Exploring Board Game AI Algorithms: Minimax

Published on 15 June 2024

Computers are very good at playing board games. Traditionally for games like Chess, algorithms like Minimax and Alpha-Beta Pruning were used to search for moves. More recently, techniques like Monte-Carlo Tree Search and Reinforcement Learning have made these AIs more formidable.

To learn more about these algorithms, I decided to implement them from scratch. These algorithms can be applied to most board games. I chose Connect Four because it is simpler than a game like Chess or Go, but not as trivial as Tic-Tac-Toe.

For those unfamiliar, Connect Four is played on a 6x7 board where two players, White and Black (Red and Yellow are used in the original game), take turns dropping their coins into one of the columns. The first player to line up 4 of their coins wins.

Illustration of a Connect Four game A Connect Four game. Black wins with a diagonal 4-in-a-row

Making a Playable Game

My approach when writing code is to write the simple solution first, then spend time making it better. This stops me from over-generalizing the solution early on, and provides the necessary context for optimizations later. For Connect Four, we only need three things to make a playable game:

Representing the Board

We use a 2D array to represent the board. We set a cell to a player's value to indicate that the player's coin is in that cell. A value of 0 indicates an empty cell.

nrows = 6
ncols = 7

# value representing each player
white = 1
black = 2

# there are 6*7 = 42 cells
board = [
    [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0],
]

Making a Move

We place the player's coin at the bottom-most empty cell in the column.

def make_move(board, player, icol):
    for irow in range(nrows - 1, -1, -1):
        if board[irow][icol] == 0:
            board[irow][icol] = player
            return True
    
    return False

Checking Wins

There are 69 ways to get a 4-in-a-row — 24 ways horizontally, 21 vertically and 24 along the two diagonals. Here's the code to check the positive diagonal:

for irow in range(nrows - 3):
    for icol in range(3, ncols):
        if (board[irow][icol] != 0) and (board[irow][icol] == board[irow + 1][icol - 1] == board[irow + 2][icol - 2] == board[irow + 3][icol - 3]):
            return board[irow][icol]

Checking the other directions is just as easy.

With that, and a bit of code to handle player turns, we're done! We could stop here and we'd have a basic two-player game.

Creating our AI Opponent

Suppose you are now playing against an AI. You start by placing a coin in the middle column. The AI could respond by placing its coin in any one of the seven columns. How does it figure out which of those columns is the best one?

Minimax and Negamax

Consider a simplified search tree as shown, where there are only three possible responses to a move, and we search 2 moves deep. Each node represents a position that could result form a move. The numbers at the bottom represent scores for a position, where a higher score is more favourable for White, and a lower score is more favourable for Black. The blue lines represent the best move for a node.

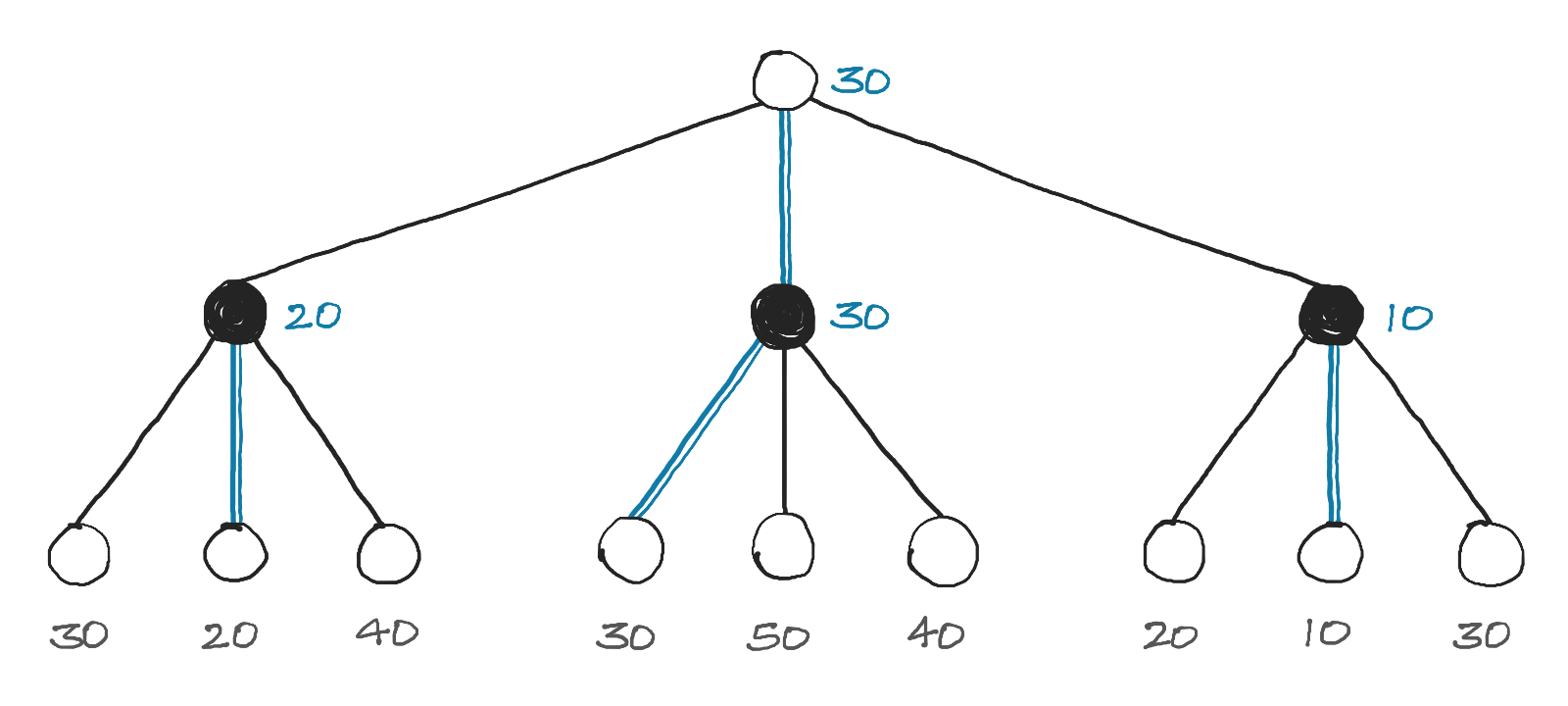Illustration of a minimax search tree Minimax search tree

A White node picks the path that leads to the highest score, while a Black node picks the path that leads to the lowest score. This way, a player can pick the best move out of all possibilities. This idea forms the basis for the minimax algorithm.

But how do we find the scores? Ideally, instead of just looking 2 moves deep, the AI should look through all possible moves until the end of the game. Depending on who wins in a position, we could assign a score (+100 for a win by White, 0 for a tie, -100 for a win by Black). But this is impractical.

Since there are 7 possible responses to any move (assuming none of the columns are filled), if the AI looks 1 move deep, that's 7 positions to consider. At 2 moves deep, that's 7² = 49 positions. At 10 moves deep, that number grows to about a quarter of a Billion. A Connect Four game can have upto 42 moves, and it turns out that there are about 4.5 Trillion unique positions! That's too much to search through.

But there's another way. Consider the position shown below, where most of White's coins are blocked but Black has several open spots. Black has a clear advantage.

Illustration of a Connect Four game Position with an advantage for Black

If we could convert this information into a score, we could limit the search depth to, say 5 moves deep, which comes out to around 16,000 positions. At the end of the search, if we haven't reached an end state (win/tie), we could use this score instead.

This is done in board games using a heuristic function, that takes in a board position and outputs a score.

Creating an accurate (and fast) heuristic is hard. I spent an ungodly amount of time trying to come up with one, and when that failed, I looked to others for inspiration:

Adam Pearce generates a score based on the number of open cells that can lead to a 4-in-a-row.
Tobias Leemann uses a pre-trained neural network as an evaluator.
Pascal Pons does not use a heuristic, since the AI computes the exact outcome of a position, made possible through tons of clever optimizations.

I ended up using a different approach. It might not be as effective as other heuristics, but it's so simple that it's crazy it even works as well as it does. We assign a value to each cell based on the number of 4-in-a-rows possible from that cell. For example, there are three ways to get 4-in-a-row from the bottom-left cell, so its value is 3.

scoremap = [
    [3, 4,  5,  7,  5, 4, 3],
    [4, 6,  8,  9,  8, 6, 4],
    [5, 8, 11, 13, 11, 8, 5],
    [5, 8, 11, 13, 11, 8, 5],
    [4, 6,  8,  9,  8, 6, 4],
    [3, 4,  5,  7,  5, 4, 3]
]

White's score is the sum of cell values for all cells containing a White coin. Black's score is obtained in a similar way. The overall score of the position is the difference between these two values. For the position shown earlier, White's score is 58 and Black's score is 66, making the total score -8, which accurately depicts an advantage for Black.

We now have everything we need to implement minimax, but there is one small inconvenice, demonstrated in the example below.

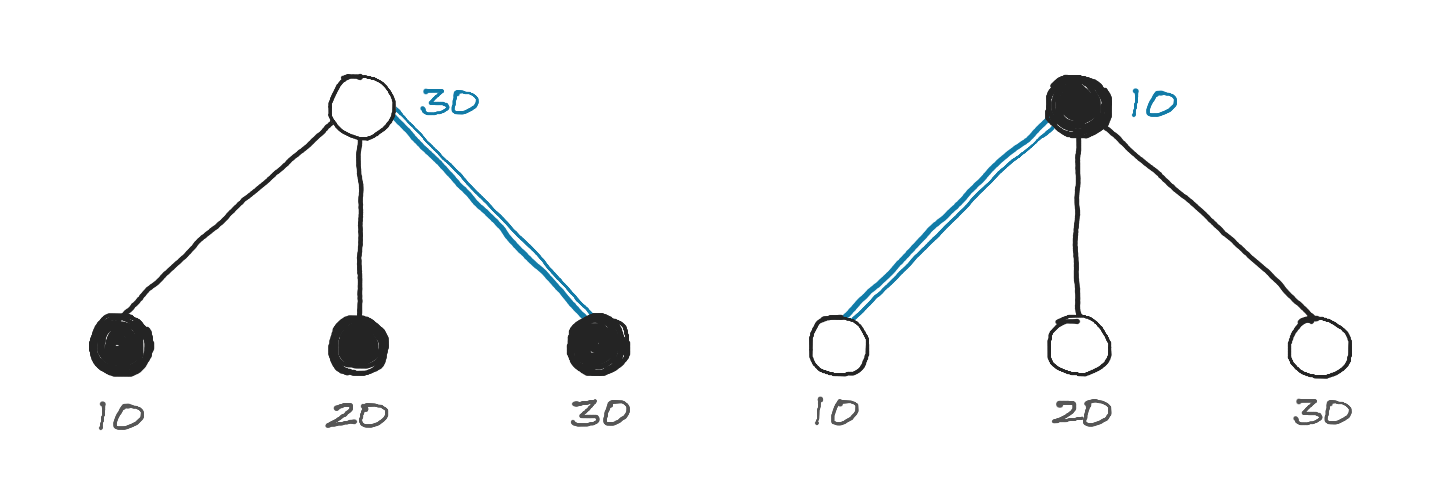Illustration of two search trees. On the left, a white node that picks the highest-valued child node. On the right, a black node that picks the lowest-valued child node. Searching one move ahead

White picks max(10, 20, 30) and Black picks min(10, 20, 30). This means we have to toggle between finding the maximum or minimum score depending on if the AI is looking at a White or Black node.

But notice that min(a, b) = -max(-a, -b). So finding min(10, 20, 30) is equivalent to finding -max(-10, -20, -30). Toggling between the players is now as simple as flipping the signs. This idea gives us the negamax algorithm, a variant of minimax that is identical in every way except that it has a simpler implementation.

def negamax(board, player, depth):
    if depth == 0 or end_state_reached(board):
        return evaluate(board), -1
    
    best_score = -1_000_000
    best_move  = 0
    
    sign = 1 if (player == white) else -1
    
    for icol in range(ncols):
        # skip filled columns
        if board[0][icol] != 0:
            continue
        
        make_move(board, player, icol)
        score = negamax(board, switch(player), depth - 1)[0]
        undo_move(board, player, icol)

        score *= sign
        if score > best_score:
            best_score = score
            best_move  = icol
    
    best_score *= sign
    return best_score, best_move

We need an undo_move since make_move modifies the board and we don't want that modification to be permanent.

With that, we have a pretty decent AI. I can just about squeeze a win at a search depth of 4, but the AI gets the better of me at greater depths (I'm not very good at this game). It's more fun to have the AIs fight each other.

In fact, the game that was shown at the very start of this post is what happened in a Depth 6 vs Depth 7 match. Despite the slight disadvantage of going second, Black won because it was able to search to a greater depth and find stronger moves.

Making the AI Stronger

On my Apple M1 running Python 3.10, it takes about 20 seconds for the AI to make a move at depth 8. It takes much longer at the start, and gets faster as more moves are made, since the time taken depends on how many positions the AI has to evaluate. Here's what that looks like at various depths:

Depth	Mean Evals	Mean Time (sec)	Evals / sec
5	7,783	0.092	84,597
6	50,656	0.588	86,149
7	376,705	4.368	86,241
8	1,979,791	23.198	85,343

Mean Time at Depth 8: 23.2 sec

There are two clear candidates for improvement: Reducing Mean Evals and increasing Evals/sec.

Optimization #1
Searching Fewer Nodes with Alpha-Beta Pruning

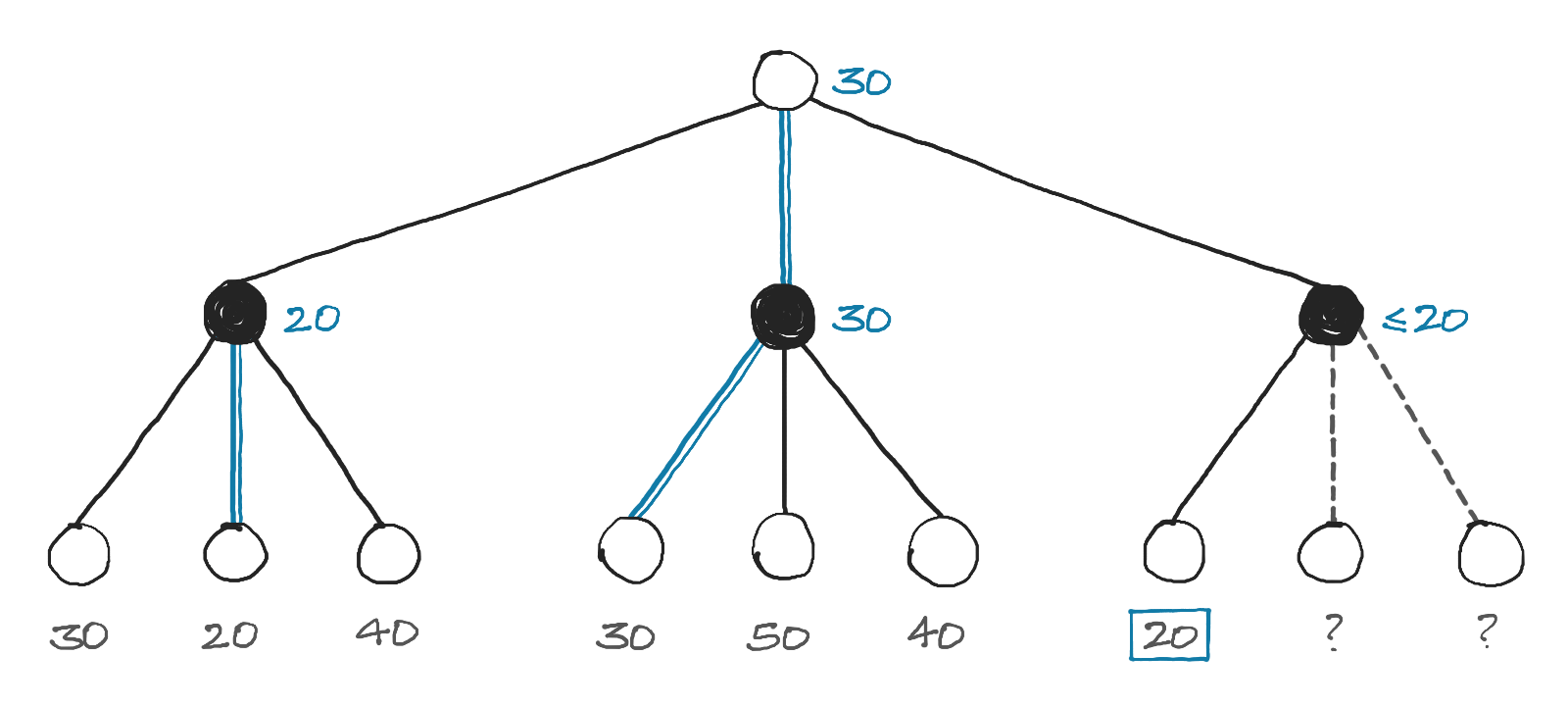Illustration of a minimax search tree with two pruned branches Pruning two branches of the search tree

Let's look at the minimax search tree again. As we evaluate nodes from left to right, notice what happens when we reach the highlighted node (with value 20). The Black node's value is set to 20 since that's the lowest score found so far. There are now two possibilies:

If either of the two remaining nodes have a value less than 20, the Black node's value will be updated to this lower value.
If the two remaining nodes have a value greater than or equal to 20, the Black node's value will remain unchanged.

In either case, without evaluating the two remaining nodes, we can be certain that the value of the Black node will be less than or equal to 20. Since that's the case, White (which wants to maximize its score) will never choose this path, since it already has a path that guarantees a score of 30. This means we can completely ignore those two child nodes. So instead of evaluating 9 nodes, we only have to evaluate 7. This seems like a minor improvement, but the benefits pile up as the search depth increases.

In simpler terms, we ignore or prune branches of the search tree that can only lead to a worse score, but still explore paths that could lead to a better score. This technique is called alpha-beta pruning.

Learning and implementing this took me quite a while, but here's the gist of how I went about it. Instead of using just one value to track the best score, we use two — alpha, the current player's best score and beta, the opponent's best score.

For example, if the current player is White, alpha starts at -infinity and can increase as we find better moves, and beta starts at +infinity and can decrease as the opponent finds better moves. When alpha >= beta, we've reached a situation as shown in the example and we don't need to search any further.

def negamax(board, player, alpha, beta, depth):
    ...
    for icol in range(ncols):
        ...
        score = negamax(board, switch(player), beta, alpha, depth - 1)[0]
        ...

        if sign*score > sign*alpha:
            alpha = score
            best_move = icol

        if sign*alpha >= sign*beta:
            break

    return alpha, best_move

Comparing regular minimax to minimax with alpha-beta pruning, we see a huge reduction in the number of evaluations:

Depth	Mean Evals minimax	Mean Evals alpha-beta
5	7,783	1,422
6	50,656	3,484
7	376,705	18,597
8	1,979,791	37,656

That's 50x fewer nodes at depth 8! The speed improves by almost the same factor.
Mean Time at Depth 8: 0.51 sec

The best part about alpha-beta pruning is that the moves found will be the exact same as regular minimax, it just does so by searching fewer nodes.

Optimization #2
Speeding up Evaluations with Bitboards

If you'd like a thorough explanation of bitboards and how to implement them for Connect Four, check out this excellent resource.

The basic idea is this — instead of using an array, we will use a 64-bit number to represent the game board. This data structure, called a bitboard, is commonly used in board games to efficiently represent the game state. The bits (numbered 0 to 63) are laid out as shown:

  6 13 20 27 34 41 48   55 62   
 —————————————————————          
│ 5 12 19 26 33 40 47 │ 54 61   
│ 4 11 18 25 32 39 46 │ 53 60   
│ 3 10 17 24 31 38 45 │ 52 59   
│ 2  9 16 23 30 37 44 │ 51 58   
│ 1  8 15 22 29 36 43 │ 50 57   
│ 0  7 14 21 28 35 42 │ 49 56 63
 —————————————————————

A cell can have one of three states — It's either empty, has a White coin, or has a Black coin. We can represent this using two bitboards, one for each player. The entire game state can now be represented with just these values:

bitboards = [
    0b0000000000000000000000000000000000000000000000000000000000000000,
    0b0000000000000000000000000000000000000000000000000000000000000000
]
counter = 0
heights = [0,  7, 14, 21, 28, 35, 42]
# bit positions for the top padding row
pad_top = [6, 13, 20, 27, 34, 41, 48]

We increment counter each time a move is made. If its value is even, the current player is White, else Black. The heights array stores the bit position for the next free cell in each column. Notice that if a column is full, its value in the heights array will match the value in the pad_top array.

This compact representation allows for optimizations that makes things faster. Making a move is now as easy as:

def make_move(state, icol):
    # set the appropriate bit for the current player to 1
    bitboards[counter & 1] ^= (1 << heights[icol])

    counter += 1
    heights[icol] += 1

Checking for wins is also much more efficient. For instance, lets consider the positive diagonal. Notice from the way we've laid out the bits, that the positive diagonal cells differ by a value of 8. For example, the bit to the top-right of bit 14 is bit 22. So for each bit, we can look at the bits that are 8, 16 and 24 bits away, and if they are all set to 1, we have a 4-in-a-row along the positive diagonal.

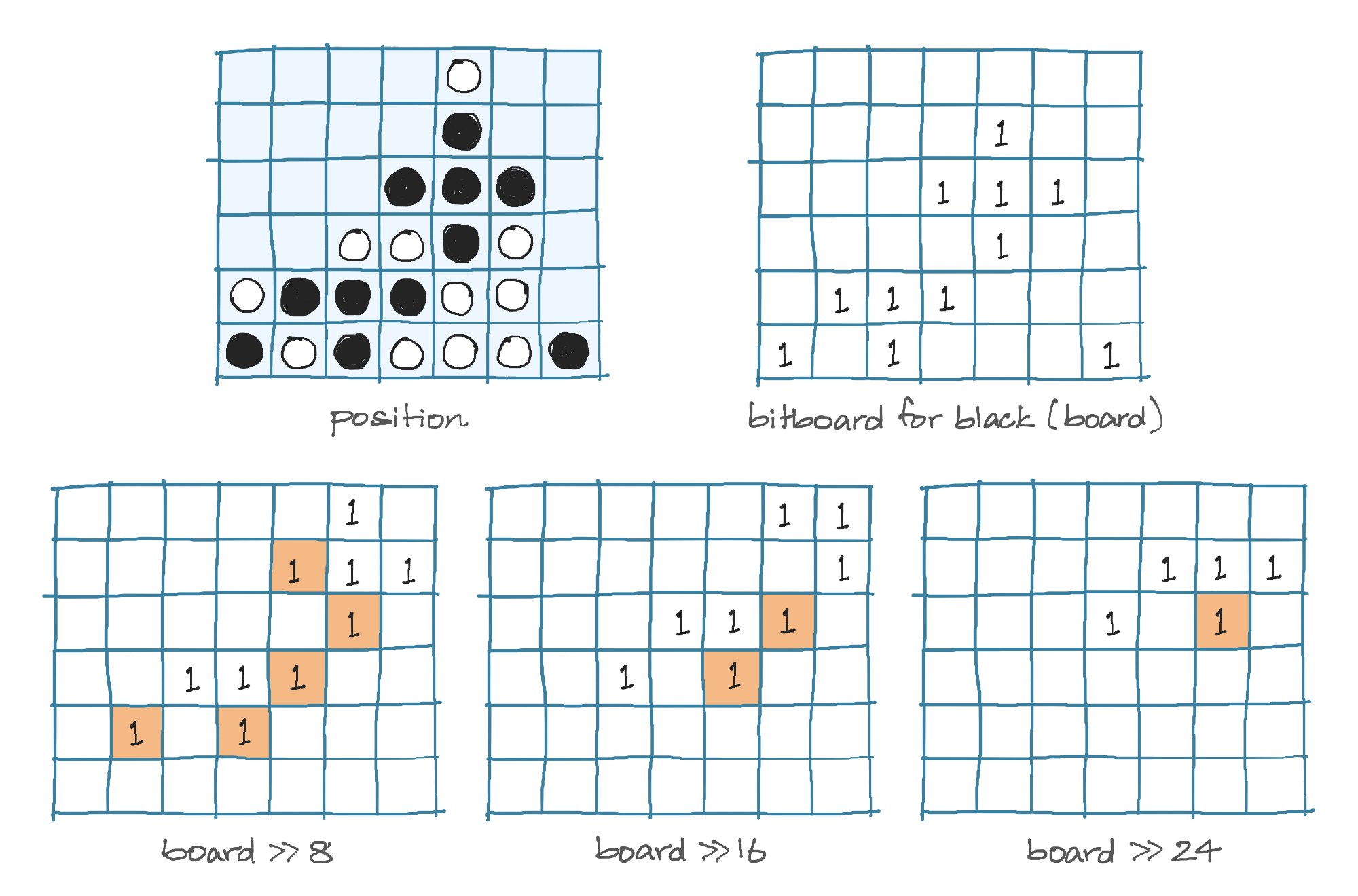
Illustration showing the process for finding four-in-a-row using bitboards

We can actually check this for every bit simultaneously, as shown above. Highlighted in orange are the bits that are in common so far. Notice that if there is a 4-in-a-row, there will be atleast one non-zero bit at the end. The implementation is as shown:

board = bitboards[1] # bitboard for Black
if board & (board >> 8) & (board >> 16) & (board >> 24) != 0: 
    return 1 # 1 indicates a win for Black

We can do the same for the other directions. For example, the horizontal cells differ by a value of 7. We can check the offsets 7, 14 and 21 to find horizontal wins.

With these optimizations, our AI is almost twice as fast.

Depth	Mean Time 2d-array	Mean Time bitboard
5	0.018	0.010
6	0.046	0.024
7	0.236	0.126
8	0.509	0.268

Mean Time at Depth 8: 0.27 sec

Comparing mean times at depth 8, we have ended up almost 100x faster than our original minimax implementation! There are ways to speed up the AI even more, but I decided to stop here.

Web Demo

I ported the code over to C++, which ended up being around 250x faster than our fastest Python implementation! I compiled it to WebAssembly and created a web interface. View the source code or play directly on your browser.

Play the Demo

What Next?

If you're interested in more optimization techniques, check out this resource. It's worth noting that a lot of these optimizations work better with a good heuristic. While our simple heuristic works to some extent, it fails to provide an accurate evaluation for more complex positions. Moving beyond Connect Four, there are board games for which creating a good heuristic is nearly impossible.

In a follow-up blog post, I'll explore a completely different technique to creating the AI, one that does not require a heuristic at all. DeepMind used this technique as part of their AlphaGo AI to achieve a breakthrough result in 2016.